Topological defects in Cartan Media

One way to do a showcase of topological defects is to try emulate a simple field theory topological defect. So take a polar field theory in 2D. That would be a $d=2$ and $G=SO(2)$ Cartan media. So I can try to come up with a configuration that imitates defects like:

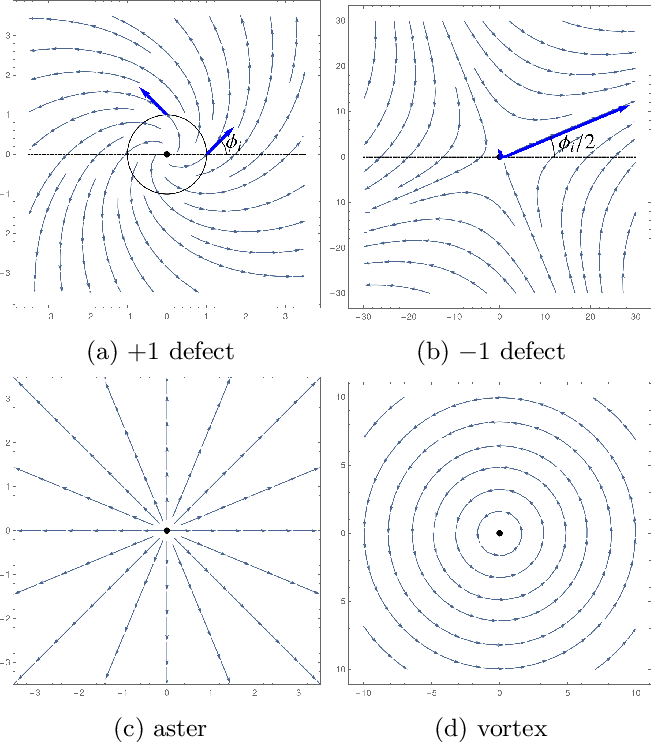
The way to do it is to simply construct $\Phi$ explicitly (which should be possible using polar coordinates), and then simply computing the generalised strain. You should be able to do this analytically, and doing so will probably tell you something about the nature of generalised strains with topological defects.

What would be doubly cool is if you can then also add some dynamics on top of this, and use it to simulate defects that attract each other etc.

In the context of simple polar field theories in 2D or 3D, elementary undergrad vector calculus is useful. I think a field with topological defects correspond to a non-conservative vector field.

• However, there is a slight subtlety here. A conservative vector field is one for which there exists a scalar such that $\mathbf{v}=\nabla \varphi$. In our case, the vector field is $\Phi :M\to SO(2)$. We are not really concerned with the integrability of $\Phi$ (that is, if there exists a scalar such that $\Phi =\nabla \varphi$), rather we are concerned with whether the generalised strains are integrable.
• This is a bit confusing of course, because in the image above I can clearly define a $\Phi$, and can compute its generalised strain, which would presumably integrate back to $\Phi$. By definition, the generalised strains should obey integrability no?
• There must be some kind of subtlety involving the point defects.
• Actually, since $SO(2)$ is abelian and $d=1$, the generalised strain fields are scalars, and the spatial integrability condition is ${\partial }_u{X}_v={\partial }_v{X}_u$. Could it be that $X_u=X_v$? That is, the generalised strain is in general irrotational, but not conservative since it has the topological defects.
  • I don’t think so. The vorticity of a SO(2) field is not always zero. Specifically it is $w_z=\sin (\theta ){\partial }_v\theta +\cos (\theta ){\partial }_u\theta =\mathbf{v}\cdot (X_u{X}_v{)}^T$.
  • We have $X_u={\partial }_u\theta$ and $X_v={\partial }_v\theta$.
  • So in this case I don’t think there is any real connection between the notion of conservative vector fields and topological defects.
    • Of course, fields with topological defects are not conservative. But not all non-conservative fields have topological defects (a field with non-zero vorticity but no singularities for example).

From what I gather, the above example does accommodate topological defects. However, they do not really relate to the failure of spatial integrability. Well, more precisely, we have that $X_u$ and $X_v$ satisfy spatial integrability everywhere but at the defect. So it is a matter of spatial integrability failure of course.

Ah! But now I get it. What happens to $\theta$ at the defect? It becomes multi-valued! (It’s not pointing in any direction / pointing in all directions). The question is what is the value of $X_u$ and $X_v$ at the defect? It should probably be the limiting value of ${\partial }_u\theta$ and ${\partial }_v\theta$ in the $u$ and $v$ directions respectively.

You can compute

$$\begin{array}{rl}{\partial }_u\theta & =-\frac{v}{u^2+v^2}\\ {\partial }_v\theta & =\frac{u}{u^2+v^2}\end{array}$$

So it seems that for any fixed value of $v$ the limit of ${\partial }_u\theta$ is well-defined, and vice-versa for ${\partial }_v\theta$. So if we define the generalised strain as

$$\begin{array}{rl}{X}_u& ={\Phi }^{-1}\underset{h\to 0}{\lim }\frac{\Phi (u+h,v)-\Phi (u,v)}{h}\\ X_v& ={\Phi }^{-1}\underset{h\to 0}{\lim }\frac{\Phi (u,v+h)-\Phi (u,v)}{h}\end{array}$$

we essentially have a definition that allows for topological defects. And if we compute them we see that $X_u{|}_{u=0,v=0}=X_v{|}_{u=0,v=0}=0$. NOTE: not correct. check those equations again

Now, if we integrate up from the Lie algebra to the Lie group, we will recover the correct $\Phi$, but it will be multi-valued at the origin. This is of course because the spatial integrability of the generalised strain does not hold at the origin. We have that

$$\frac{{\partial }^2\theta }{{\partial }_u{\partial }_v}=\frac{v^2-u^2}{u^4+2u^2{v}^2+v^4}$$

which diverges at the origin.

So the nice thing about the Cartan media framework is that, though $\Phi$ is ill-defined at the topological defects, the generalised strains are well defined (as long as you use the limit definition above) and smooth.

Notes:

• It seems that $X_u=0$ along the line $v=0$, and vice versa for $X_v$. So the zeros of $X_u$ and $X_v$ essentially form a cross in the material base space, and the topological defect is located where the two lines meet. This could probably used to locate defects in numerics.

A more interesting case is when you have a line defect. For example, for nematic fluids in 3D: 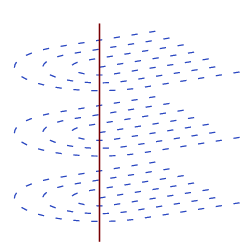This would still involve a singularity of some sort, but along a line.

Constructing the initial condition

We want to construct an initial condition with a $k=+1$ and a $k=-1$ topological defect. Let’s say the are located at $(0,0)$ and $(u_s,0)$ respectively. I think the best way to do this is to consider a dynamical system

$$\begin{array}{rl}\dot{x}& =f(x,y)\\ \dot{y}& =g(x,y)\end{array}$$

for which the Jacobian at $(0,0)$ is stable and rotational, and at $(u_s,0)$ is a saddle. The result will of course not be normalised, but hopefully after you have normalised it will all work okay.

---

References

• A field theory of dislocations in a COSSERAT continuum (Hermann Schaefer)
• MAXWELL’s equations for dislocations moving in a COSSERAT continuum (Hermann Schaefer)